EM算法
具体例子为Gaussian Mixture Model,由k个component组成。
$$P(z_k = 1) = \pi_k, \sum_k\pi_k = 1, 0 \le \pi_k \le 1$$
$$P(x|z) = \prod_k\mathcal{N}(x|\mu_k,\Sigma_k)^{z_k}$$
$$P(x) = \sum_zP(z)P(x|z) = \sum_k\pi_k\mathcal{N}(x|\mu_k,\Sigma_k)$$

高斯混合模型有两种求法，一种是拿最大似然的形式求导，另外一种就是用隐含变量的形式来看待。

######直接拿似然求导
拿似然求导。
先写出似然函数$\ln P(X) = \sum_n\ln(\sum_k\pi_k\mathcal{N}(x_n,\mu_k,\Sigma_k))$，注意到其中的约束条件为$\sum_k\pi_k = 1$
首先注意到$$\mathcal{N}(x_n|\mu_k,\Sigma_k) = \frac{1}{(2\pi)^{\frac{d}{2}}}\frac{1}{|\Sigma_k|^{\frac{1}{2}}}\exp (-\frac{1}{2}(x_n-\mu_k)^T\Sigma^{-1}(x_n-\mu_k))$$
利用$\frac{\partial X^TAX}{\partial X} = A^TX + AX$

对$\mu_k$求导，得到
$$\frac{\partial \ln P(x)}{\partial \mu_k} = \sum_n\frac{\pi_k\mathcal{N}(x_n|\mu_k,\Sigma_k)}{\sum_j\pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j)}\Sigma^{-1}(x_n-\mu_k)$$
令梯度为0，并令$$r(z_{nk}) = \frac{\pi_k\mathcal{N}(x_n|\mu_k,\Sigma_k)}{\sum_j\pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j)} $$得到$$\mu_k = \frac{1}{N_k}\sum_nr(z_{nk})x_n$$

$$N_k = \sum_nr(z_{nk})$$

最为复杂的是对$\Sigma_k$进行求导，我们看$Gaussian$分布对$\Sigma_k$求导的结果。$Gaussian$对数概率密度函数为
$$\ln L = \ln \mathcal{N}(x|\mu,\Sigma) -\frac{d}{2}\ln 2\pi - \frac{1}{2}\ln|\Sigma| -\frac{1}{2}(x - \mu)^T\Sigma^{-1}(x - \mu)$$

那么前面一项$\ln |\Sigma|$对$\Sigma$求导得到
$$\frac{\partial -\frac{1}{2}\ln |\Sigma|}{\partial \Sigma} = -\frac{1}{2}\Sigma^{-1}$$

后面一项$$J = -\frac{1}{2}(x - \mu)^T\Sigma^{-1}(x - \mu) = Tr(\Sigma^{-1}S)$$
其中$$S = (x-\mu)(x-\mu)^T$$
$$\frac{\partial J}{\partial \Sigma_{ij}} = \frac{\partial Tr(\Sigma^{-1}S)}{\Sigma_{ij}} = -\frac{1}{2}Tr(\frac{\partial \Sigma}{\Sigma_{ij}}S) = -\frac{1}{2}Tr(-\Sigma^{-1}\frac{\partial \Sigma}{\partial \Sigma_{ij}}\Sigma^{-1}S) = \frac{1}{2}\Sigma^{-1}S\Sigma^{-1}$$

所以得到对$\Sigma$求导结果为$\frac{\partial L}{\partial \Sigma} = -\frac{1}{2}\Sigma^{-1} + \frac{1}{2}\Sigma^{-1}S\Sigma^{-1}$
令导数为0，得到$\Sigma = S$

所以在混合高斯中对$\Sigma_k$进行求导，依据上面的求导，稍微有点不同的是前面是对数似然求导，而现在不是对数求导，其实也一样，只要利用$\frac{\partial L}{\partial x} = \frac{\partial e^{\ln L}}{\partial x}$得到即可

所以得到
$$\Sigma_k = \frac{1}{N_k}\sum_{n}r(z_{nk})(x_n - \mu_k)(x_n-\mu_k)^T$$

对$\pi_k$求导，并引入拉格朗日乘子，得到$$\frac{\partial \ln P(x)}{\partial \pi_k} = \sum_n\frac{\mathcal{N}(x_n|\mu_k,\Sigma_k)}{\sum_j\pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j)} + \lambda$$
令梯度为0,并两边同乘$\pi_k$，然后对k进行求和，得到$\lambda = N$,
所以
$$\pi_k = \frac{N_k}{N}$$
因为每个变量都是相互依赖的，所以该式没有解析解。所以对高斯混合模型来说分为两步。

1. E步，求出$r(z_{nk})$
2. M步，依据上面推导出来的式子对$\mu,\Sigma,\pi$等参数进行更新。

######以隐含变量的角度来看待
EM是一种通用的方法，来对含有隐藏变量的分布来求似然。
首先要写出完全概率，也就是$P(x,z)$
在GMM中，
$$P(x,z) = \prod_n\prod_k(\pi_k\mathcal{N}(x_n|\mu_k,\Sigma_k))^{z_{nk}}$$

$$\ln P(x,z) = \sum_n\sum_kz_{nk}(\ln \pi_k + \ln \mathcal{N}(x_n|\mu_k,\Sigma_k))$$

关于z的信息，只有后验分布$P(z|x)$
直接最大化似然$P(x,z)$非常直接。但是我们的目标不是最大化似然联合分布。所以我们考虑在$P(z|x)$分布下的后验期望，也就是$Q$函数。
$$Q(\theta,\theta^{old}) = \sum_zP(z|x,\theta^{old})\ln P(x,z|\theta)$$

接下来最大化$Q$函数即可。
根据贝叶斯公式
$$P(z|x) \propto \prod_n\prod_k(\pi_k\mathcal{N}(x_n|\mu_k,\Sigma_k)^{z_{nk}}$$

根据上式，$P(z|x)$是可以分解的独立的。
所以$$E[z_{nk}] = \frac{\sum_{z_k}z_{nk}(\pi_k\mathcal{N}(x_n|\mu_k,\Sigma_k))^{z_{nk}}}{\sum_{z_{nj}}z_{nj}(\pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j))^{z_{nj}}}$$

$$=\frac{\pi_k\mathcal{N}(x_n|\mu_k,\Sigma_k)}{\sum_j\pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j)} = r(z_{nk})$$

所以
$$E_Z[\ln P(x,z)] = \sum_n\sum_kr(z_{nk})(\ln \pi_k + \ln \mathcal{N}(x_n|\mu_k,\Sigma_k))$$

同样对$\pi_k$求导，并引入拉格朗日乘子，得到
$$\pi_k = \frac{1}{N}\sum_nr(z_{nk})$$

同理对$\mu_k,\Sigma_k$求导也得到和上述式一样

EM的证明：
$$\ln P(X|\theta) = L(q,\theta) + KL(q || p)$$

$$L(q,\theta) = \sum_zQ(z)\ln \frac{P(x,z|\theta)}{Q(z)}$$

$$KL(q||p) = \sum_z-Q(z)\ln \frac{P(z|x,\theta)}{Q(z)}$$
在E步中，使用$Q(z) = P(z|x,\theta)$,然后KL消失，此时$\ln P(x|\theta) = L(q,\theta)$
M步极大化该函数，提高了似然值。
所以似然值是不断增加的。

实现代码：EM

注意在实现的时候，初始化参数很重要，如果一开始的$\mu$随机初始化的化，结果会比较差，即使迭代步数够多。比如说这是一开始产生的点：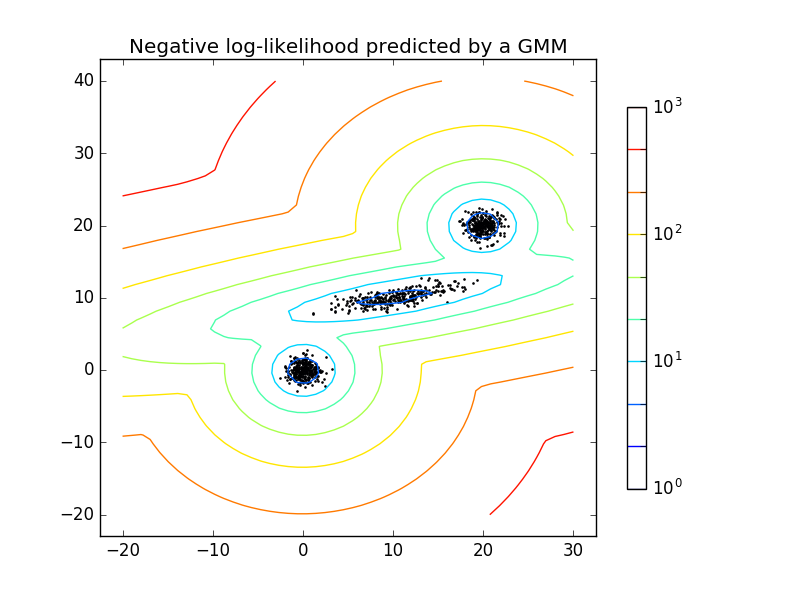

然后随机初始化最后得到的结果：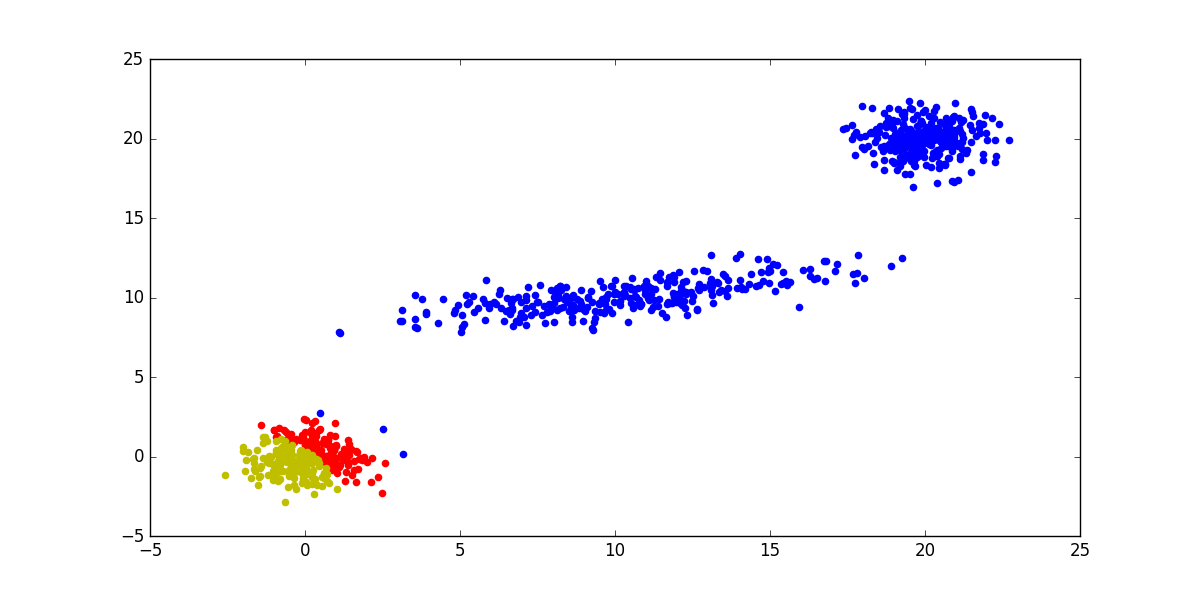

如果初始化初始在各自的中心的结果：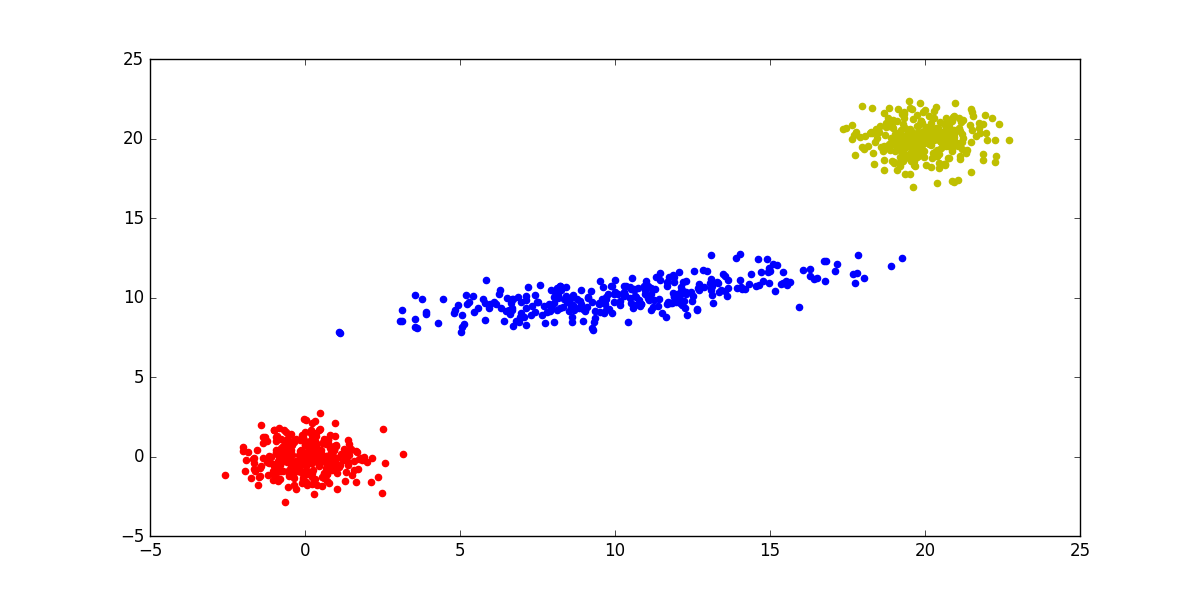

所以有在EM之前可以做一下KMeans.

Reference:

PRML Chapter 9
scikitlearn