高斯过程

对于基本的线性回归，我们会假设$f(x)$的一个形式，比如说$f(x) = mx + c$或者$f(x) = ax^2 + bx + c$等等，然而高斯过程不直接假设函数的形式，而是让数据自己说话，对函数的分布进行推断。即后验$p(f|D)$，但是对函数后验$p(f|D)$分布进行推断比较困难，我们对这些函数在$x_1, x_2, \cdots, x_n$上的值进行推断。高斯过程即假设$p(f(x_1), f(x_2), \cdots,f(x_n))$是一个多元高斯分布，均值为$\mu(x)$,方差为$\Sigma(x)$,其中$\Sigma_{ij} = k(x_i, x_j)$,$k(x_i, x_j)$是核函数，中心思想是$x_i, x_j$如果相似的话$k(x_i, x_j)$应该达到最大，这样意味着$f(x_i)$与$f(x_j)$高度相关，使得函数变得平滑。通常核函数$k(x_i, x_j)$的选择是
$$k(x_i, x_j) = \sigma^2\exp(\frac{(x_i-x_j)^2}{-2l^2})$$

称作squared exponential kernel

对于高斯过程来说，通常$\mu(x)$选择都是$0$

现在假设训练数据为$x,f$,测试集为$x_*, f_*$,$f_*$是我们需要预测的，一开始只知道$x_*$.根据先前的假设
$p(f,f_*) \sim \mathcal{N}(x|0,\Sigma)$
将$\Sigma$可分为四部分
$$\Sigma = \begin{bmatrix}K& K_* \\ K_*& K_{**}\end{bmatrix}$$

其中K为训练集之间的$k(x_i,x_j), (x_i,x_j \in Train)$, $K_*$为$k(x_i,x_j)(x_i\in Train, x_j \in Test)$，$K_{**}$为$k(x_i,x_j)$
根据后面的高斯性质,那么有$p(f_*|f) \sim \mathcal{N}(x|\mu_*,\Sigma_*)$，其中
$$\mu_* = K_*K^{-1}f$$
$$\Sigma_* = K_{**} - K_*K^{-1}K_*$$

对于预测的$f_*$，可以认为$f_* = \mu_*$

对于有添加了高斯噪声的预测，即$t = f + \epsilon$,其中$\epsilon \sim \mathcal{N}(x|0, \beta^{-1}I)$

那么$p(t|f) \sim \mathcal{N}(x|f,\beta^{-1}I)$,而$p(f)$根据高斯过程的定义有$p(f) \sim \mathcal{N}(x|0,\Sigma)$

所以有
$$p(t) = \int p(t|f)p(f)df$$

两个都是高斯，根据高斯的性质，有$p(t) \sim \mathcal{N}(x|0, C)$,其中$C_{ij} = \Sigma_{ij} + \beta^{-1}\delta_{ij}$

其余的后验均值和方差都和没有噪声的类似。

对于参数的估计$\theta = {\sigma, l}$可以采用最大似然的方式。

$$\frac{\log p(f|x, \theta)}{\partial \theta_i} = -\frac{1}{2}Tr(\Sigma^{-1}\frac{\partial \Sigma}{\partial \theta_i}) + \frac{1}{2}f^T\Sigma^{-1}\frac{\partial \Sigma}{\partial \theta_i}\Sigma^{-1}f$$

实现

实现代码如下：
GaussianProcess

效果图：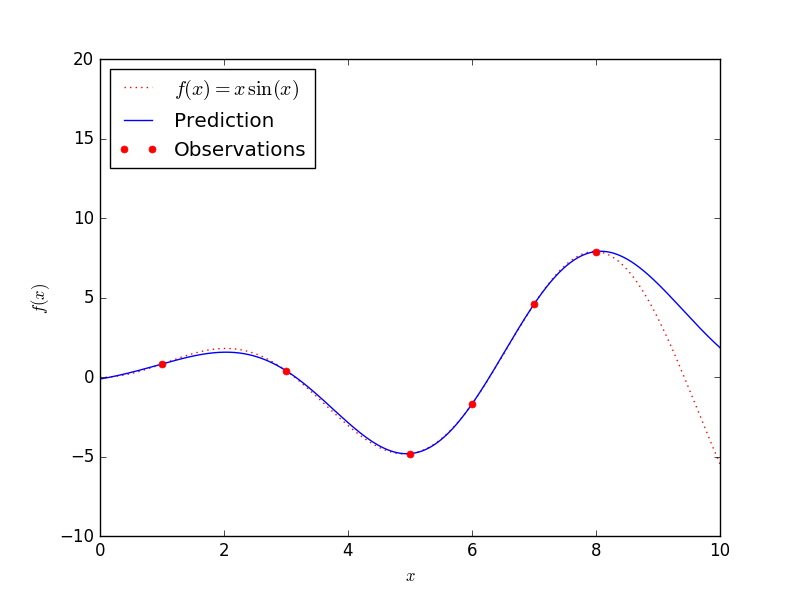

从图中看还是能很好的拟合预测的数据的。

高斯性质

两个基本Gaussian性质，对于多元高斯$x \sim N(x|\mu, \Sigma)$,将$x$分为$x_a, x_b$两部分。对于条件高斯$p(x_a|x_b)$，仍然是高斯。
证明：
可以单看$\exp$部分的$x_a$的部分。因为
$$p(x) = \frac{1}{(2\pi)^{\frac{D}{2}}}\frac{1}{|\Sigma|^{\frac{1}{2}}}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))$$

对于$\exp$里面的二次项$-\frac{1}{2}x^T\Sigma^{-1}x$，以及一次项$x\Sigma^{-1}\mu$ 反应了$x$的均值以及方差
所以对于$p(x_a|x_b)$可以单看$x_a$的二次项和一次项即可决定$p(x_a|x_b)$的形式。有二次项一定是高斯分布，因为无论怎样都可以进行配方，配成高斯的形式然后加上归一化因子即可。
对于$p(x_a|x_b)$里面$\exp$部分，可以将$x_b$看做固定值，我们首先进行分块，令$x^T = [x_a^T,x_b^T]$, $\Sigma = \begin{bmatrix}\Sigma_{aa}&\Sigma_{ab}\\\Sigma_{ba}&\Sigma_{bb}\end{bmatrix}$,$\Sigma^{-1} = \begin{bmatrix}\Lambda_{aa} & \Lambda_{ab} \ \Lambda_{ba} &\Lambda_{bb}\end{bmatrix}$，注意到$\Sigma_{aa}^{-1}$是不等于$\Lambda_{aa}$的
原式$\exp$里面的形式可以化为
$$-\frac{1}{2}(x_a-\mu_a)^T\Lambda_{aa}(x_a-\mu_a)-\frac{1}{2}(x_a-\mu_a)^T\Lambda_{ab}(x_b-\mu_b)\\
-\frac{1}{2}(x_b-\mu_b)^T\Lambda_{ba}(x_a-\mu_a)-\frac{1}{2}(x_b-\mu_b)^T\Lambda_{bb}(x_b-\mu_b) \quad (1)$$

把$x_a$有关的二次项和一次项几区出来，我们可以得到二次项为$-\frac{1}{2}x_a^T\Lambda_{aa}x_a$,一次项为$x_a^T(\Lambda_{aa}\mu_a - \Lambda_{ab}(x_b-\mu_b))$，所以得到$$\Sigma_{a|b} = \Lambda_{aa}^{-1}$$
$$\mu_{a|b}=\Lambda_{aa}^{-1}(\Lambda_{aa}\mu_a- \Lambda_{ab}(x_b-\mu_b))=\mu_a-\Lambda_{aa}^{-1}\Lambda_{ab}(x_b-\mu_b)
$$

然后根据
$$\left( \begin{array}{cc} A & B\\C & D\end{array}\right)^{-1} = \left(\begin{array}{cc}M & -MBD^{-1}\\-D^{-1}CM & D^{-1}+D^{-1}CMBD^{-1}\end{array}\right) \quad(2)$$

其中$M = (A-BD^{-1}C)^{-1}$，所以我们得到$\Lambda_{aa}=(\Sigma_{aa}-\Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba})^{-1}$，$\Lambda_{ab}=-(\Sigma_{aa}-\Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba})^{-1}\Sigma_{ab}\Sigma_{bb}^{-1}$

根据以上，得到
$$\mu_{a|b} = \mu_a+\Sigma_{ab}\Sigma_{bb}^{-1}(x_b-\mu_b)$$

$$\Sigma_{a|b}= \Sigma_{aa}-\Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba}$$

高斯的边缘分布，也是高斯
$p(x_a) = \int p(x_a,x_b)dx_b$，为了将$x_b$积掉，首先在原式中对$x_b$进行配方，提出与$x_b$有关的所有项为
$$-\frac{1}{2}x_b^T\Lambda_{bb}x_b + x_b^T(\Lambda_{bb}\mu_b - \Lambda_{ba}(x_a-\mu_a))$$

将此式进行完全配方，得到
$$-\frac{1}{2}(x_b-\Lambda_{bb}^{-1}m)^T\Lambda_{bb}(x_b-\Lambda_{bb}^{-1}m) + \frac{1}{2}m^T\Lambda_{bb}^{-1}m$$

其中
$$m = (\Lambda_{bb}\mu_b -\Lambda_{ba}(x_a-\mu_a))$$

对$x_b$进行积分，可以根据Gaussian得到为一个常数，并且和$x_a$无关。积分后留下来和$x_a$有关的项为$\frac{1}{2}m^T\Lambda_{bb}^{-1}m$
根据$(1)$式，以及留下来的式子得到与$x_a$有关的项为
$$\frac{1}{2}(\Lambda_{bb}\mu_b - \Lambda_{ba}(x_a-\mu_a))^T\Lambda_{bb}^{-1}(\Lambda_{bb}\mu_b -\Lambda_{ba}(x_a-\mu_a))\\ -\frac{1}{2}x_a^T\Lambda_{aa}x_a + x_a^T(\Lambda_{ab}\mu_b + \Lambda_{aa}\mu_a) + const$$

整理一下得到
$$-\frac{1}{2}x_a^T(\Lambda_{aa} - \Lambda_{ba}\Lambda_{bb}^{-1}\Lambda_{ba})x_a + x_a^T(\Lambda_{aa} - \Lambda_{ba}\Lambda_{bb}\Lambda_{ab})\mu_a + const$$

所以$$\Sigma_{a}=(\Lambda_{aa}-\Lambda_{ba}\Lambda_{bb}^{-1}\Lambda_{ba})^{-1}$$

均值为
$$\Sigma_a(\Lambda_{aa}-\Lambda_{ba}\Lambda_{bb}^{-1}\Lambda_{ba})\mu_a =\mu_a$$

而根据上面的$(2)$式，得到$(\Lambda_{aa}-\Lambda_{ba}\Lambda_{bb}^{-1}\Lambda_{ba}) = \Sigma_{aa}$

所以$p(a)$边缘分布也为高斯分布$E[a] = \mu_a, cov[a] = \Sigma_{aa}$