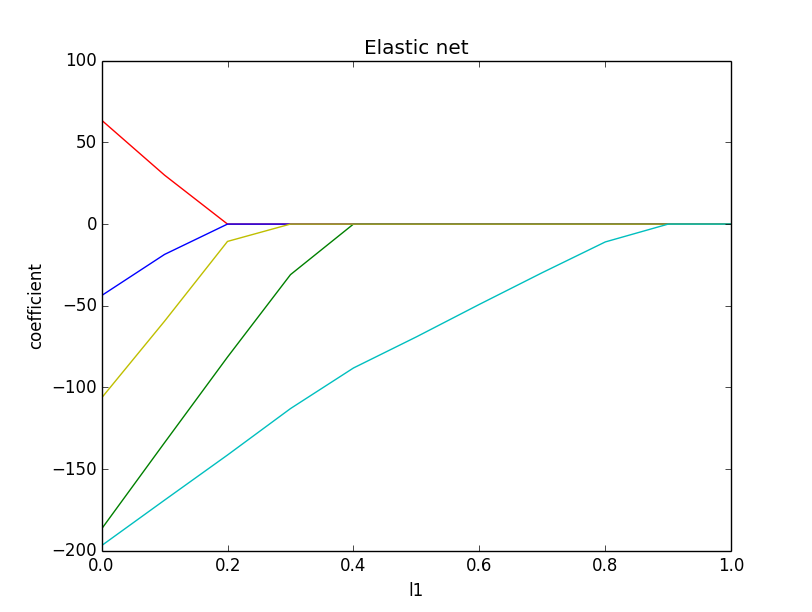
Linear Regression with Elastic Net
线性回归
线性回归最简单的形式为
$$y = wx$$
损失函数为
$$L(y,x;w) = \frac{1}{2n}\sum_{i}||y_i - w^Tx_i||_2^2$$
这个问题可以直接求解,令梯度为0,得到
$$w = (X^TX)^{-1}X^Ty$$
但是通常来说$(X^TX)$不是满秩的,数值计算上会有问题,将会有无穷多个解,所以通常在损失函数$L$上加上$||w||_2^2$,就是通常所说的ridge regression.但是最近发现稀疏化能够有效的减少特征,所以为了让特征数更好,可以加上$||w||_1$,变成lasso regression.如果两种综合起来,即加上$\lambda_2||w||_2^2 + \lambda_1||w||_1$。最后的损失函数的形式为:
$$L(x,y;w) = \frac{1}{2n}\sum_i||y_i-w^Tx_i||_2^2 + \lambda_2||w||_2^2 + \lambda_1||w||_1$$
称作Elastic Net。但是当存在$||w||_1$的时候,对$L$求导可能存在不可导的情况。为了解决这种问题,我们采用proximal method。
注意到以往的梯度更新算法有
$$x_{k+1} = x_{k} - t_k\nabla f(x_{k})$$
我们将$f(x)$在$x_k$处泰勒展开得到,令$\nabla^2 f(x_k) = \frac{1}{t_k}I$:
$$\bar{f}(x) = f(x_k) + \nabla f(x_k)^T(x-x_k) + \frac{1}{2t_k}||x-x_k||_2^2$$
整理得到
$$\bar{f}(x) = \frac{1}{2t_k}||x-(x_k -t_k\nabla f(x_k))||_2^2 + c$$
c是常数,注意到之前的更新其实就是$$x_{k+1}= \mathop{\arg\min}_x \bar{f}(x)$$
上述对$L$可抽象为$\min L(x) = f(x) + g(x)$,其中$f(x)$可导,$g(x)$在某些地方不可导。将$f(x)$在$x_k$处二阶展开。同先前的一样
$$\bar{L}(x) = \frac{1}{2}||x - (x_k - t_k\nabla f(x_k))||_2^2 + t_kg(x)$$
所以更新的时候采用$x_{k+1} = \mathop{\arg\min}_x\bar{L}(x)$
所以定义$prox_h(x) = \mathop{\arg\min}_u(\frac{1}{2}(u-x)^2 + h(u))$
如果$h(x) = 0, prox_h(x) = x$,如果$h(x) = t||x||_1$,那么根据子梯度有$0 \in (x-u) + \partial h(u)$,如果$u > 0$,那么有$0 = u - x + t \rightarrow u = x - t$,如果$u < 0$,有$u = x + t$,如果有$u = 0$,有$x \in [-t, t]$,所以
如果$h(u) = t||u||_1$,那么
$$prox_h(x) = \begin{cases} x - t& \text{if } x > t \\ 0 & \text{if } x \in[-t, t] \\x + t & \text{if } x < -t\end{cases}$$
所以当$h(x) = \lambda_1||x||$,
$$prox_h(x) = sign(x)(|x|-\lambda_1)_+
$$其中$(x)_+ = \max(x,0)$
同理当$h(x) = \lambda_2||x||$的时候,
$$prox_h(x) = \frac{1}{1 + \lambda_2}x$$
当$h(x) = \lambda_1||x||_1 + \lambda_2||x||_2^2$的时候,
$$prox_h(x) = \frac{1}{1 + \lambda_2}sign(x)(|x|-\lambda_1)_{+}$$
对于上面的
$$L(x,y;w) = \frac{1}{2n}\sum_i||y_i-w^Tx_i||_2^2 + \lambda_2||w||_2^2 + \lambda_1||w||_1$$
其中$f(x) = \frac{1}{2n}\sum_i||y_i - w^Tx_i||_2^2$,$g(x) = \lambda_1||w||_1 + \lambda_2||w||_2^2$。但是注意到因为有一个学习速率$t_k$,即对$f(x)$做二阶泰勒展开的时候假设$\nabla^2f(x_k) = \frac{1}{t_k}I$,为了去掉$t_k$,与$prox_h(x)$一致,其中$g(x)$就变为了$g(x) =t_k\lambda_1||w||_1 + t_k\lambda_2||w||_2^2$
实现代码如下:Elastic Net
我们分别取不同的l1参数,可以发现l1参数确实有稀疏化的作用