常用分类方法的一种,对于训练数据来说,每次找到最优的一个特征,对该特征进行划分。划分之后得到不同的子集,再分别在不同的子集进行划分,直到满足某个划分标准则停止。
如何选择最优的特征有不同的算法。
常见的决策树算法有ID3,C4.5算法,对于ID3算法,采用信息增益最大的特征来选择最优的特征。
算法流程如下:对于在未划分之前,首先算出该数据集$D$的熵。假设该数据集有$K$类,训练集大小为$N$.其中属于第$j$类的样本数为$D_j$那么熵
$$Entropy(D) = \sum_{k}\frac{D_k}{N}\log_2\frac{D_k}{N}$$
对于选择某个特征$s$,它将数据集划分成为$t$个不相交的子集,其中每个子集大小为$N_t$,每个子集中,属于第$j$类的样本数为$D_{tj}$,那么对该特征划分的信息增益为
$$Gain(s) = Entropy(D) - \sum_{t}\frac{N_t}{N}(\sum_{k}\frac{D_{tj}}{N_t}\log_2\frac{D_{tj}}{N_t})$$
C4.5相比ID3算法有两个改进
- ID3算法会倾向于选择取值比较多的特征(从上面的式子可以看出,取值较多的熵容易较小,与之对应的是信息增益会变得更多)
- ID3没办法处理连续值的属性(C4.5将连续值划分成两个部分$\ge v_i$与$< v_i$)
C4.5采用的是信息增益率最多的特征作为划分的特征。
即$$Gain_{ratio}(s) = \frac{Gain(s)}{Entropy(D)}$$
后面采用了ID3实现了一下。
实现代码:DecisionTree
利用自己造的数据,最后生成出来的决策树利用matplotlib画图如下: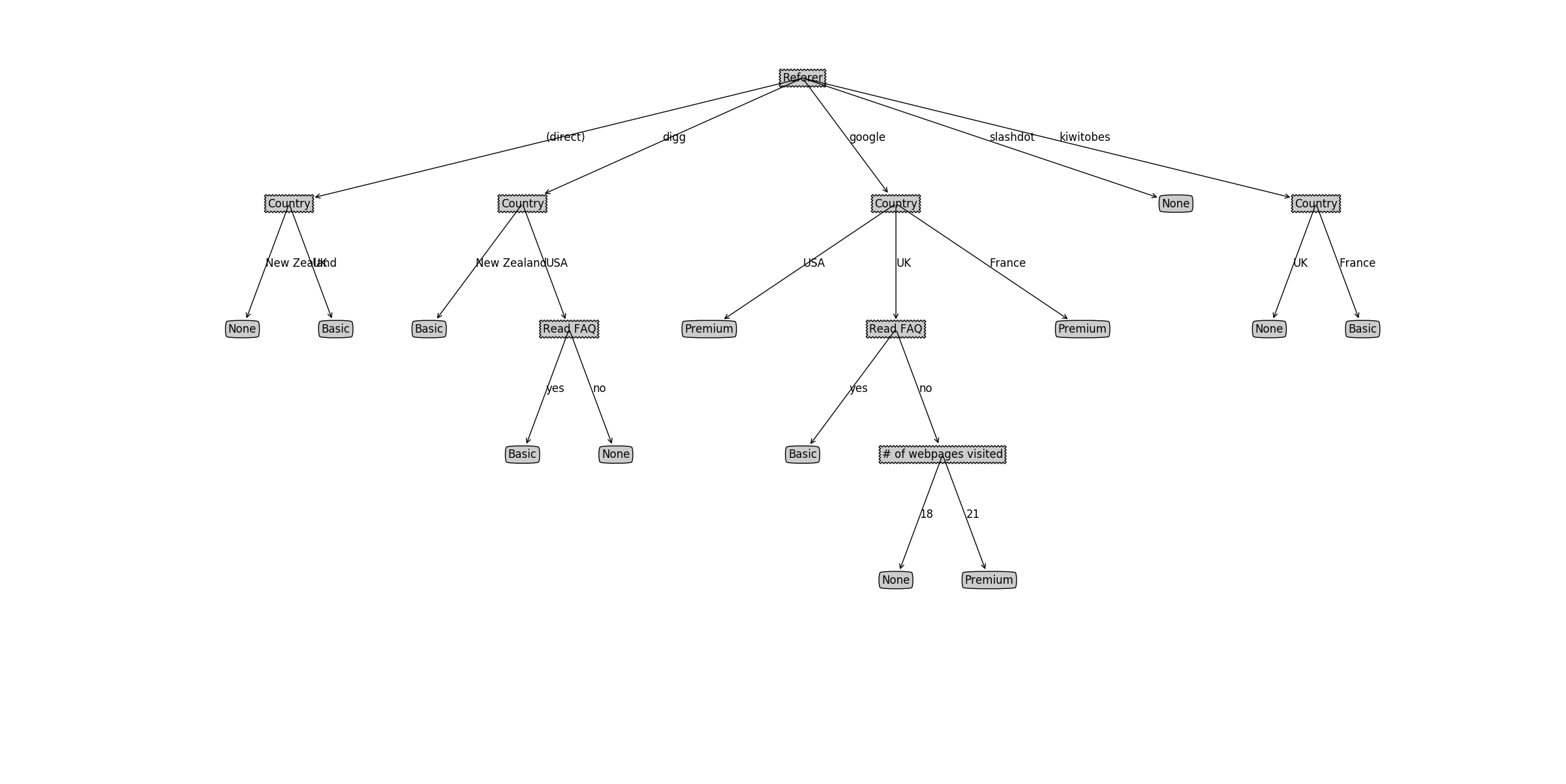
除了ID3和C4.5以外,还有CART(classification and regression trees)算法。
对于regression, 选择的标准是均方误差最小。在划分特征的时候,首先选择一个特征$j$,然后选择特征值$s$,将数据集划分为$R_1 = {x_i|x_i^{(j) \ge s}}$, $R_2={x_i|x_i^{(j)} < s}$,然后找到最优变量$j,s$使得
$$\mathop{\arg \min}_{j,s}(\mathop{\min}_{c1, c2}(\sum_{x_i \in R_1}(y_i - c_1)^2 + \sum_{x_i \in R_2}(y_i - c_2)^2))$$
找到之后继续划分即可。
而对于classification,采用的是基尼指数。假设样本有$K$类,其中第$k$类的概率为$p_k = \frac{N_k}{N}$那么该样本的基尼指数是
$$Gini(D) = \sum_{k}p_k(1 - p_k)$$
化简一下可以得到
$$Gini(D) = 1 - \sum_{k}p_k^2$$
在选择特征的时候,首先选择第一个特征$j$,然后选择特征值$A_j$,可以将数据集分为两部分,特征值等于$A_j$的$D_1$与不等于$A_j$的$D_2$,那么在特征$A_j$下的基尼指数为
$$Gini(D, A_j) = \frac{|D_1|}{N}Gini(D_1) + \frac{|D_2|}{N}Gini(D_2)$$