Adaboost算法
boost的思想是组合一堆弱分类器来组成一个强分类器,Adaboost便是其中一个最著名的例子。
Adaboost的推导可以由以下式子来完成:首先Adaboost是一堆弱分类器的组合,可以写为$f_m(x) = \frac{1}{2}\sum_{j}^m\alpha_jy_j(x)$,它的损失函数采用loss损失函数,所以最终可以写为:
$$L(x) = \sum_i^n\exp(-t_if_m(x_i)) = \sum_{i}^n\exp(-t_i\frac{1}{2}\sum_{j}^m\alpha_jy_j(x_i))$$
其中$x_i$为训练数据, $t_i$为label,$t_i \in {+1, -1}$
现在我们假设前$m - 1$分类器已经训练好了。现在要训练第$m$个分类器,损失函数可以化为如下形式:
$$L(x) = \sum_{i}^n\exp(-t_i\frac{1}{2}\alpha_my_m(x_i))\exp(-t_if_{m-1}(x_i))$$
后面一项是已经固定了训练好的分类器,我们设为$w_{i}^m = \exp(-t_if_{m-1}(x_i))$。所以损失函数为
$$L(x) = \sum_{i}^nw_i^m\exp(-\frac{1}{2}t_i\alpha_my_m(x_i))$$
对于那些$y_m(x)$分对的数据$x_i \in C(x)$, 有$t_iy_m(x_i) = 1$。对于那些分错的数据$x_i \in W(x)$,有$t_iy_m(x_i) = -1$,所以损失函数可以写成如下形式:
$$L(x) = \sum_{i \in C(x)}w_i^me^{-\frac{\alpha_m}{2}} + \sum_{i \in W(x)}w_i^me^{\frac{\alpha_m}{2}}$$
现在为了将形式统一起来,并且想到要写成loss形式$I(y_m(x_i), t_i)$, 所以我们添加一项$\sum_{i \in W(x)}w_i^me^{-\frac{\alpha_m}{2}}$。前面加上这项,后面减去这项,$L$就可以写为
$$L(x) = (e^{\frac{\alpha_m}{2}} - e^{-\frac{\alpha_m}{2}})\sum_{i=1}^nw_i^mI(t_i \neq y_m(x_i)) + \sum_{i=1}^nw_i^me^{-\frac{\alpha_m}{2}}$$
在优化$y_m(x)$的时候,与后一项无关,只与$\sum_iw_i^mI(t_i \neq y_m(x_i))$有关,所以训练分类器以这个指标为基础。
对于$\alpha_m$的更新,可以对$L(x)$求导即可。
$$\frac{\partial L}{\partial \alpha_m} = (\frac{1}{2}e^{\frac{\alpha_m}{2}} + \frac{1}{2}e^{-\frac{\alpha_m}{2}})\sum_{i=1}^nw_i^mI(t_i\neq y_m(x_i)) - \frac{1}{2}\sum_{i=1}^nw_i^me^{-\frac{\alpha_m}{2}}$$
令梯度为0,我们可以得到如下方程:
$$e^{\frac{\alpha_m}{2}}\sum_{i=1}^nw_i^mI(t_i\neq y_m(x_i)) = e^{-\frac{\alpha_m}{2}}(\sum_{i=1}^nw_i^m-\sum_{i=1}^nw_i^mI(t_i\neq y_m(x_i)))$$
两边同除$\sum_{i=1}^nw_i^m$,并令$\epsilon_m = \frac{\sum_{i=1}^nw_i^mI(t_i \neq y_m(x_i))}{\sum_{i=1}^nw_i^m}$,得到
$$e^{\frac{\alpha_m}{2}}\epsilon_m = e^{-\frac{\alpha_m}{2}}(1 - \epsilon_m)$$
求解得到$$\alpha_m = \ln \frac{1 - \epsilon_m}{\epsilon_m}$$
现在$w_i^{m + 1} = \exp(-t_if_{m}(x_i)) = \exp(-t_if_{m-1}(x_i))\exp(-\frac{1}{2}t_i\alpha_my_m(x_i)) = w_i^m\exp(-\frac{1}{2}t_i\alpha_my_m(x_i))$
然后利用$t_iy_m(x_i) = 1 - 2I(t_i \neq y_m(x_i))$
所以$w_i^{m+1} = w_i^m\exp(-\frac{\alpha_m}{2})\exp(\alpha_mI(t_i \neq y_m(x_i)))$
根据以上式子,我们采用分类器为简单的决策树分类器,即只有一个节点的决策树。代码如下:
做一个二维决策面如下图所示: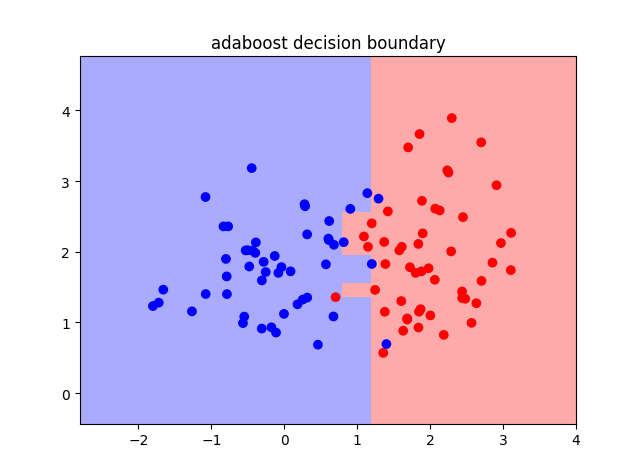
Adaboost的优缺点:
优点:泛化错误率低,易编码,可以应用在大部分分类器上,无参数调整。
缺点:对离群点敏感。
适用数据类型:数值型和标称型数据。