最近终于把RNN的求导细节给弄明白了,写一篇文章来总结一下DNN,CNN以及RNN的具体求导细节。
在网上搜索资料的同时,发现很多时候RNN的求导大多数给的是矢量化的形式,并不容易去理解,比如说$y$是一个标量,$y = \sum_n||y_n - t_n||^2$,通常用的error形式,对一个权重矩阵$w$求导,也应该是一个矩阵的形式。但是一旦涉及到微积分的链式法则,通常很难以去理解。比如说
$$\frac{\partial y}{\partial W} = \frac{\partial y}{\partial z}\frac{\partial z}{\partial W}$$
其中z为一个vector,那么$\frac{\partial z}{\partial W}$应该是一个矩阵吗?还是一个vector?始终没有弄明白,所以自己总结了一下以一种比较容易理解的方式(对单个权重值去求导),$\frac{\partial y}{\partial W_{ij}}$求出之后,再将其矢量化,就非常容易去理解了。文中图片均来自网上。
微积分链式法则
首先注意到微积分的链式法则。如果一个变量和求导的变量有关联,需要对所有相关的变量都求导。
Example:
$$z_2 = 4 * z_1$$
$$z_3 = 3 * z_1 + 5 * z_2$$
当我们求$\frac{\partial z_3}{\partial z_1}$的时候,不能只考虑到$z_1$在$z_3$里面单纯的出现过,而把$z_2$视作常数。
所以$\frac{\partial z_3}{\partial z_1} = 3 + \frac{\partial z_2}{\partial z_1}$,其中前面的3为当前本身求导所得,后面的为和$z_1$有关的项所得。
MLP
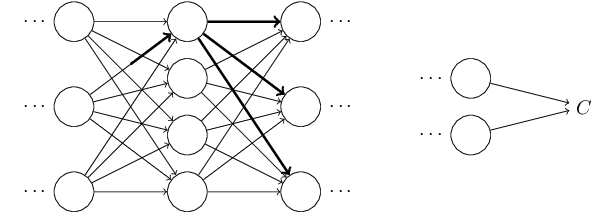
约定以下符号:输入为$x$,其中维度为$d_1$,第l层的节点数为$d_l$
每一层对于每一个节点有$l \ge 2$,其中$a_i^1 = x_i$
$$z_i^l = \sum_{j=1}^{d_{l-1}}w^l_{ij}a_j^{l-1} + b_i^l$$
$$a_i^l = \sigma(z_i^l)$$
最后一层为L层。最终的误差为,其中$y$为正确类标的vector
$$C = ||y - a^L||_2^2 = \frac{1}{2}\sum_{i=1}^{d^L}(y_i - a_i^L)^2$$
对于bp算法,定义$\delta_i^l = \frac{\partial C}{\partial z_i^l}$。bp算法的核心思想就在于求$\delta_i^l$,通过求$\delta_i^l$,我们就可以很容易求得对于$W,b$等参数的导数
注意到$\sigma \prime(x) = (1 - \sigma(x))\sigma(x)$
首先对于顶层的
$$\delta_i^L = \frac{\partial C}{\partial z_i^L} = \frac{\partial C}{\partial a_i^L}\frac{\partial a_i^L}{z_i^L} = (a_i^L - y_i)(1 - a_i^L)a_i^L \quad (1)$$
对于不是顶层的$\delta_i^l$,首先注意到$z_i^l$通过权重$W_{ij}^{l+1}$影响到了$l + 1$层的所有节点。所以在求$\frac{\partial C}{\partial z_i^l}$的使用使用链式法则如下:
$$\delta_i^l = \frac{\partial C}{\partial z_i^l} = \sum_{j=1}^{d^{l+1}}\frac{\partial C}{\partial z_j^{l+1}}\frac{\partial z_j^{l+1}}{\partial z_i^l}$$
其中前面一项已经求得为$\delta_j^{l+1}$,后面一项
$$\frac{\partial z_j^{l+1}}{\partial z_i^l} = \frac{\partial z_j^{l+1}}{\partial a_i^l}\frac{\partial a_i^l}{\partial z_i^l} = W^{l+1}_{ji}(1 - a_i^l)a_i^l$$
综合以上得到
$$\delta_i^l = \sum_{j=1}^{d^{l+1}}\delta_j^{l+1}W^{l+1}_{ji}(1 - a_i^l)a_i^l \quad (2)$$
在得到以上式子之后对参数进行求导就十分容易了
$$\frac{\partial C}{\partial W^l_{ij}} = \frac{\partial C}{\partial z_i^l}\frac{\partial z_i^l}{\partial w^l_{ij}} = \delta_i^la_j^{l-1} \quad (3)$$
$$\frac{\partial C}{\partial b^l_i} = \frac{\partial C}{\partial z_i^l}\frac{\partial z_i^l}{\partial b_i^l} = \delta_i^l \quad (4)$$
以上为DNNbp算法的4个核心式子。现在将他们矢量化:以前带有下标的现在都以向量表示,参照以上(1234),$\odot$表示点乘
$$\delta^L = (a^L - y)\odot\sigma\prime(a^L) \quad (1)$$
$$\delta^l = ((W^{l+1})^T\delta^{l+1})\odot\sigma\prime(a^l) \quad (2)$$
$$\frac{\partial C}{\partial W^l} = (\delta^l)^Ta^{l-1} \quad (3)$$
$$\frac{\partial C}{\partial b^l} = \delta^l \quad (4)$$
CNN
CNN相比DNN而言,为了处理平移不变性,使用了权重共享的方式。为了处理旋转不变性,使用了pooling的方式。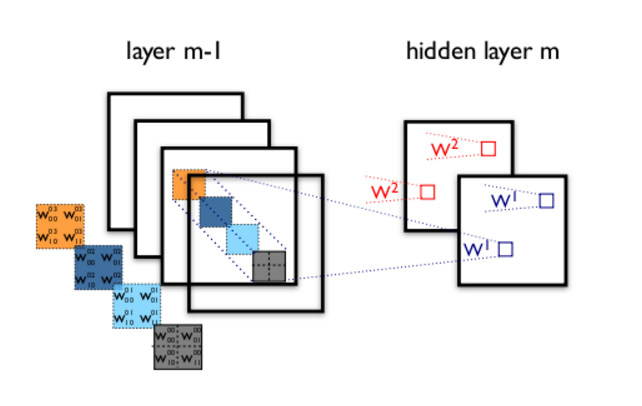
LeNet:通常的卷积神经网络的结构如下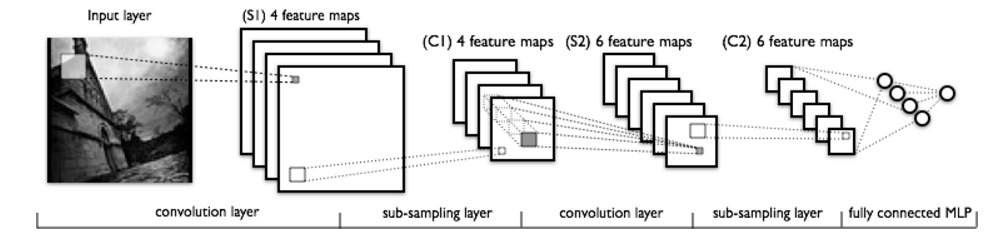
符号:
层首先分为卷积层和pooling层。
$a^{kl}_{ij}$表示第$l$层的第$k$个feature map的第$i$行$j$列像素。
假设第l层的feature map有$f_l$个,如果下一层为卷积层,其中卷积核的大小为$k_l$。那么权重$w$总共有$f_l \times f_{l+1}$个,以LeNet为例,$C1 \rightarrow S2$的$W$就有$4 \times 6 = 24$个权重需要学习。其中$w_{ab}^{sk(l+1)}$表示第$l$层的第$s$个feature map对$l + 1$层的第$k$个feature map坐标为$a,b$的权重。
$$z^{k(l+1)}_{ij} = \sum_{s=0}^{f_l-1}\sum_{a=0}^{k_l-1}\sum_{b=0}^{k_l-1}w_{ab}^{sk(l+1)}a^{sl}_{(i+a)(j+b)} + b^{k(l+1)}\quad (1)$$
第$l$层有
$$a_{ij}^{k(l+1)} = \sigma(z_{ij}^{k(l+1)}) \quad(2)$$
如果下一层为pooling层,此处采用mean-pooling,pooling大小为$2 \times 2$
那么$$a_{ij}^{k(l+1)} = \frac{1}{4}\sum_{a=0}^{1}\sum_{b=0}^1a^{kl}_{(2i-a)(2j-b)} \quad (3)$$
最后将层数连接一个全连接层,也就是将所有feature map展平,和上面的MLP一样。
对于全连接层的$\delta$求法和上面一样,不细述了。现在有区别于MLP的是pooling层和convolutional层。
通常在最后pooling层之后接上全连接的输出层,对于全连接的输出层$\delta^L$如前面MLP所示。同样的$\delta^{L-1} = ((W^{L})^T\delta^{L})\odot\sigma\prime(a^L)$
当$L-2$层为pooling层的时候,泛化到一般也就是当$\delta^l$为pooling层的时候,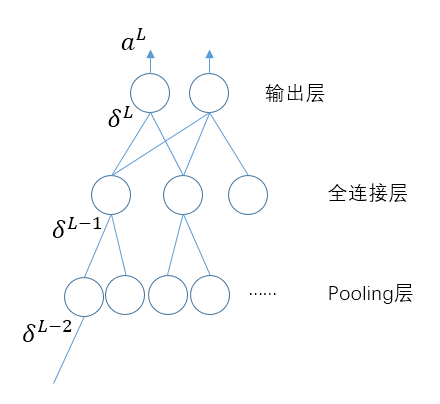
其中$\delta^{l+1}$层已知,那么根据(3)
$$\delta^{kl}_{ij} = (1 - a_{ij}^{kl}) * (a_{ij}^{kl})* \frac{1}{4} * \delta^{k(l+1)}_{pq}$$
其中$\delta^{k(l+1)}_{pq}$的下标$pq$为$ij$进行pooling之后对应的那个节点,实现方便一点的是进行上采样,也就是以前是下采样,4个节点变为一个,现在进行上采样1个节点变4个,其中这4个的$\delta$值是一样的。那么很容易的得到$pq = ij$
乘以1/4是因为我们pooling核大小为$2\times2$,如果pooling核大小为$k\times k$,那么后面为$\frac{1}{k^2}$
如果当前层为卷积层:根据(1),其中与节点$z_{ij}^{kl}$相关的节点是$z_{(i-a)(j-b)}^{k(l+1)}$,自己可以手动算一下。
那么$$\delta_{ij}^{kl} = \sum_{s=0}^{f_{l+1}-1}\sum_{a=0}^{k_l-1}\sum_{b=0}^{k_l-1}w^{ks(l+1)}_{ab}\delta_{(i-a)(j-b)}^{s(l+1)}$$
后面两项求和可以看做真正的卷积操作,因为之前的所谓的“卷积”操作只是相关操作而已。其中还有当$ij=0,0$的时候$i-a,j-b$可能出现负数,这是因为$0,0$点其实只和下一层的$0,0$点有关,这样的操作可以采样full卷积来实现,即周围填充无数个0,然后进行卷积即可。
在得到$\delta$之后,可以非常轻松的对$W,b$进行求导。注意到和$w_{ab}^{sk(l+1)}$相关的项为$ij$,其中$a \le i \le N^{kl} - k_l + a, b \le j \le N^{kl} - k_l + b$,$N^{kl}$为第$l$层第$k$个feature map的大小$N^{kl}\times N^{kl}$
$$\frac{\partial C}{\partial w_{ab}^{sk(l+1)}} = \sum_{i=a}^{N^{kl} - k_l + a}\sum_{j=b}^{N^{kl} - k_l + b}\frac{\partial C}{\partial z_{ij}^{k(l+1)}}\frac{\partial z_{ij}^{k(l+1)}}{\partial w_{ab}^{sk(l+1)}}$$
$$=\sum_{i=a}^{N^{kl} - k_l + a}\sum_{j=b}^{N^{kl} - k_l + b}\delta_{ij}^{k(l+1)}a^{sl}_{ij}$$
在实现中可以发现其实上式就是第$l+1$层的$\delta$与第$l$层的输出进行卷积操作,就可以得到对应的$W$的梯度。
同理对b的求导,类似于$w$,只不过与b相关的为所有当前层对应的$\delta$值
$$\frac{\partial C}{\partial b^{k(l+1)}}=\sum_{ij}\delta^{k(l+1)}_{ij}$$
RNN
RNN的求导其实也和CNN差不多,关键RNN是时序的,稍微有一点变形,叫做BPTT(Back Propagation Through Time)
RNN的结构如下: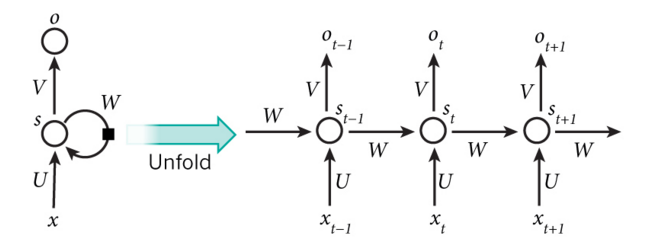
其中两个关键式子:
$$s_t = \tanh(Ux_t + Ws_{t-1}) \quad (1)$$
$$o_t = softmax(Vs_t) \quad (2)$$
其中我们的惩罚函数采用cross-entropy,其中$y_t^n$为one-hot vector,表示t时刻的vector的第n位。
$$L(o,y) = \sum_t\sum_{n}y_t^n\log o_t^n \quad (3)$$
因为vector形式求导不是很容易理解,所以我们采用标量的形式来求导,然后将其写成矢量的形式
$$z_t^i = \sum_kU_{ik}x_t^k + \sum_kW_{ik}s_{t-1}^k \quad (4)$$
$$s_t^i = \tanh(z_t^i) \quad(5)$$
$$b_t^i = \sum_kV_{ik}s_t^k \quad (6)$$
$$o_t^i = \frac{e^{b_t^i}}{\sum_je^{b_t^j}} \quad (7)$$
对于上面的$L(o,y)$可以写成$\sum_tE_t$,其中$E_t$为每个时刻的cross-entropy loss.以$E_t$为例,其中$y_t$为label,假设第$c$位为1,即$y_t^c=1$,其余位都为0.那么$E_t = -y_t^c\log o_t^c$,将$o_t^c$利用(7)式代入得到,
$$E_t = b_t^c - \log\sum_je^{b_t^j}$$
$$\frac{\partial E_t}{\partial V_{ij}} = -(s_t^j - \frac{e^{b_t^c}}{\sum_je^{b_t^j}}s_t^j) = (o_t^c - 1)s_t^j$$
上述为i == c的情况下。
如果i != c的情况,中间$b_t^c$对$V_{ij}$的导数为0,所以
$$\frac{\partial E_t}{\partial V_{ij}} = o_t^is_t^j$$
写成矢量的形式就是
$$\frac{\partial E_t}{\partial V} = o_t \otimes s_t$$,当然在$y_c=1$的地方$o_t$需要减掉1
现在设$$\delta_t^{ki} = \frac{\partial E_t}{\partial z_k^i}$$
同样以$E_t$为例,$$\delta_t^{ti} = \frac{\partial E_t}{\partial z_t^i} =\frac{\partial b_t^c}{\partial z_t^i} -\sum_k\frac{e^{b_t^k}}{\sum_je^{b_t^j}}\frac{\partial b_t^k}{\partial z_t^i}$$
如果i==c,第一项为$V_{ci}$,否则为0
$$\frac{\partial E_t}{\partial z_t^i} = (V_{ci} - \sum_ko^k_tV_{ki})(1 - (s_t^i)^2)$$
所以得到了$\delta^{ti}_t$,那么$\delta_t^{(t-1)i}$可以通过$\delta_{t}^{ti}$得到,这就是BPTT。
$$\delta_t^{(t-1)i} = \frac{\partial E_t}{\partial z_{t-1}^i} = \sum_{j}\frac{\partial E_t}{\partial z_t^j}\frac{\partial z_t^j}{\partial z_{t-1}^i} = \delta_{t}^{tj}W_{ji}(1 - (s_{t-1}^i)^2)$$
得到$\delta$之后,可以很轻松的对$W,U$求导,得到
$$\frac{\partial E_t}{W_{ij}} = \sum_k\delta_t^{ki}s_{k-1}^j$$
$$\frac{\partial E_t}{U_{ij}} = \sum_k\delta_t^{ki}x_k^j$$
至此所以推导完毕。
实现:没有采用GPU加速,当然现在有很多深度学习库,实现只针对于理解算法。
Reference
http://deeplearning.net/tutorial/lenet.html#lenet
https://en.wikipedia.org/wiki/Chain_rule
http://neuralnetworksanddeeplearning.com/chap2.html
RNN Backpropagation