给定数据$x_1,x_2,\cdots,x_N$,其中每个$x_i$是一个$D$维向量,现在要将其降低到M维,降维有以下几种方法:
PCA
PCA可以以两种方式来看待,一是最大化方差,二是最小化误差
最大化方差
考虑$D=2$的情况,假设$M=1$,找到的投影方向为$\mu_1$,那么最大化方差即为
$$\max v = \frac{1}{N}\sum_{i=1}^{N}(\mu_1^Tx_i - \mu_1^T\bar{x})^2 \quad(1)$$
其中$\bar{x} = \frac{1}{N}\sum_{i=1}^{N}x_i$,$(1)$式可以变化成为
$$\max v = \mu_1^TS\mu_1$$
$$S = \frac{1}{N}\sum_{i=1}^{N}(x_i-\bar{x})(x_i-\bar{x})^T$$
$S$为协方差矩阵,如果不对$\mu_1$进行约束的话,那么$||\mu_1||\rightarrow \infty$即可,但是我们找到是方向,所以对$\mu_1$进行大小约束,有$\mu_1^T\mu_1=1$。
所以问题转化为带有约束的最大值问题,引入拉格朗日乘子$\lambda$,得到拉格朗日函数$L(\lambda,\mu_1)=\mu_1^TS\mu_1 - \lambda(\mu_1^T\mu_1 -1)$,对$\mu_1$进行求导,令其等于0,得到
$$\frac{\partial L}{\partial \mu_1} = 2S\mu_1 - 2\lambda\mu_1 = 0$$
$$S\mu_1 = \lambda\mu_1$$
所以$\mu_1$为S的特征向量,$\lambda$为S的特征值,为了让$v=\mu_1^TS\mu_1 = \lambda$最大,所以选择$\lambda$为最大的特征值即可。
这是降为一维的情况,降为$M$维的情况可以使用归纳法证明,得到选择前$M$个最大的特征值以及对应的特征向量即可。
最小化误差
每个$x_n$可以被D个正交向量$\mu_i$所表示,即$x_n$在$\mu$所在的空间中,$\mu$为基向量。有
$$x_n = \sum_{i=1}^{D}\alpha_{ni}\mu_i \quad(2)$$
因为$\mu_i$为正交基向量,所以两边同乘$\mu_i^T$可以得到$\alpha_{ni}= x_n^T\mu_i$
$$x_n = \sum_{i=1}^D(x_n^T\mu_i)\mu_i \quad(3)$$
现在假设从其中选择$M$个正交基,然后剩下的D - M个正交基对所有$x_n$都是一样的,得到$x_n$在M个正交基的新的表示
$$\hat{x_n} = \sum_{i=1}^Mz_{ni}\mu_i + \sum_{i=M+1}^{D}\bar{b_i}\mu_i \quad (4)$$
现在要使新的$\hat{x_n}$与$x_n$的误差最小。即
$$\min J = \frac{1}{N}\sum_{i=1}^{N}||x_i - \hat{x_i}||^2 \quad(5)$$
将前面的$(3)$式带入$(5)$,得到
$$\min J = \frac{1}{N}\sum_{n=1}^{N}||\sum_{i=1}^M(x_n^T\mu_i - z_{ni})\mu_i + \sum_{i=M+1}^D(x_n^T\mu_i - \bar{b_i})\mu_i||^2$$
对$z_{ni}$求导得到$z_{ni} = x_n^T\mu_i$,对$\bar{b_i}$求导得到$\bar{b_i} = \frac{1}{N}\sum_{i=1}^{N}x_n^T\mu_i = \bar{x}^T\mu_j$
所以将得到$z_{ni}$与$\bar{b_i}$带入$J$,得到
$$J = \frac{1}{N}\sum_{n=1}^N\sum_{i=M+1}^D(x_n^T\mu_i - \bar{x}\mu_i)^2 = \sum_{i=M+1}^{D}\mu_i^TS\mu_i$$
所以同样根据归纳法可以证得$\lambda_i$为从小到大的特征值,$\mu_i$为所对应的特征向量。
PCA的几个问题:
1.对于高维数据,并且$N < D$的时候的情况,D有可能有几百万维,而N也许只有几百条数据。此时X为$N\times D$的大小,先经过均值后,$S = \frac{1}{N}X^TX$,其中$S$为$D \times D$的大小,那么整体复杂度为$O(D^3)$,是不可接受的。所以要采取一定的变换,为了求特征向量$S\mu_i = \lambda_i \mu_i$,两边同时左成$X$,得到$\frac{1}{N}XX^T(X\mu_i) = \lambda_i(X\mu_i)$,令$v_i = X\mu_i$,所以有$\frac{1}{N}XX^T = \lambda_iv_i$,而对$\frac{1}{N}XX^T$进行特征值分解的复杂度为$O(N^3)$,大大降低了复杂度,在找到$\lambda_i$和$v_i$之后,即$\mu_i \propto X^Tv_i$,为了规一化,即$\mu_i^T\mu_i=1$,得到$\mu_i = \frac{1}{(N\lambda_i)^{\frac{1}{2}}}X^Tv_i$
2.PCA是找到在正交方向上方差最大的方法,如果方差最大的方向不是正交方向的话,PCA的效果不会很好。
3.PCA是一种无监督的方法,且没有特定的参数,除了M之外,选择M的时候依据的准则一般是$\frac{\sum_{i=1}^M\lambda_i}{\sum_{i=1}^{D}\lambda_i} \ge 0.95$
4.在应用PCA的时候,也可以不降维,而使用白化操作。使得均值为0,方差为1。比如说找到了$U$和$L$,其中$U$为特征向量矩阵,L为对角阵,对角线的值为特征值,那么进行
$$y_n = L^{-\frac{1}{2}}U^T(x_n - \bar{x})$$
会得到
$$\frac{1}{N}\sum_{i=1}^{N}y_ny_n^T = \frac{1}{N}\sum_{i=1}^{N}L^{-\frac{1}{2}}U^T(x_n-\bar{x})(x_n-\bar{x})^TUL^{-\frac{1}{2}} = I$$
实现代码:
PCA
原始的点: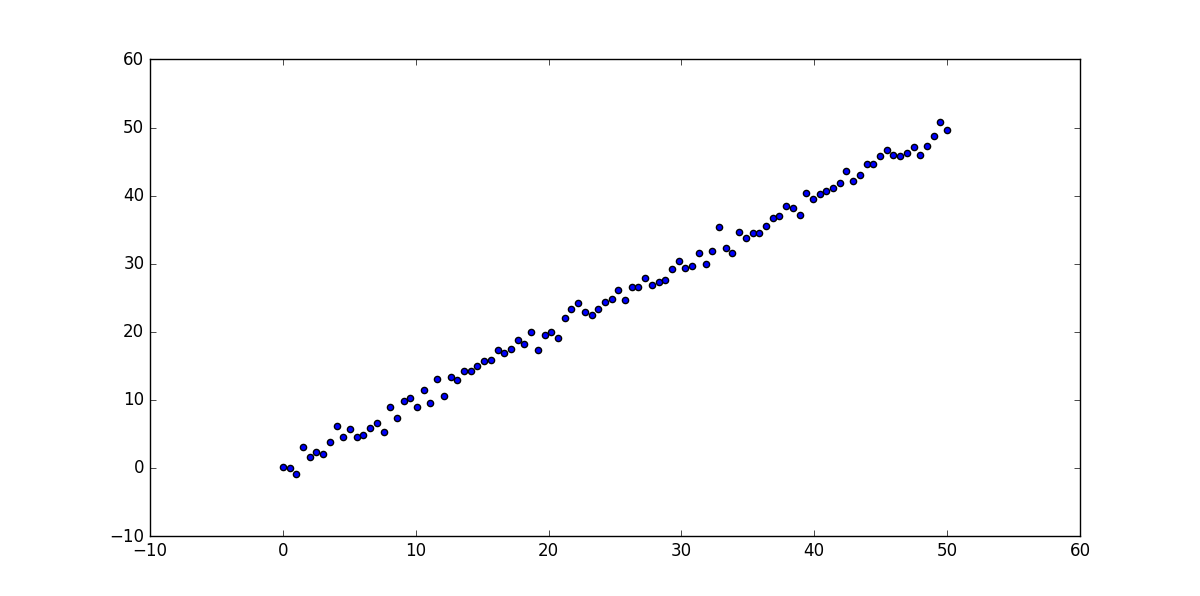
投影后的点: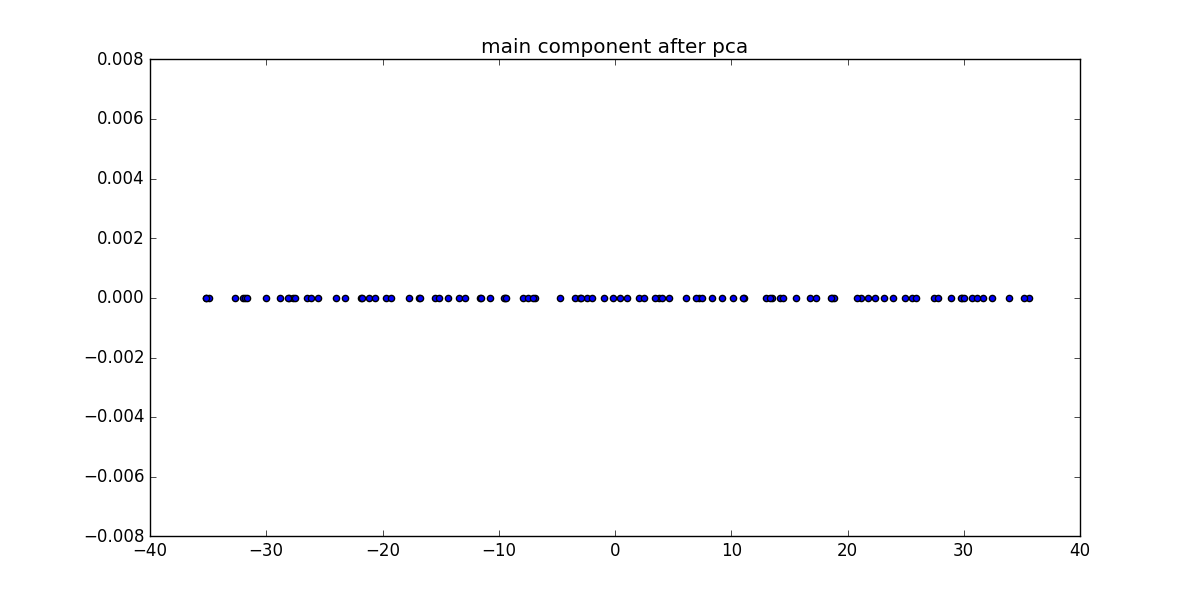
重构的点: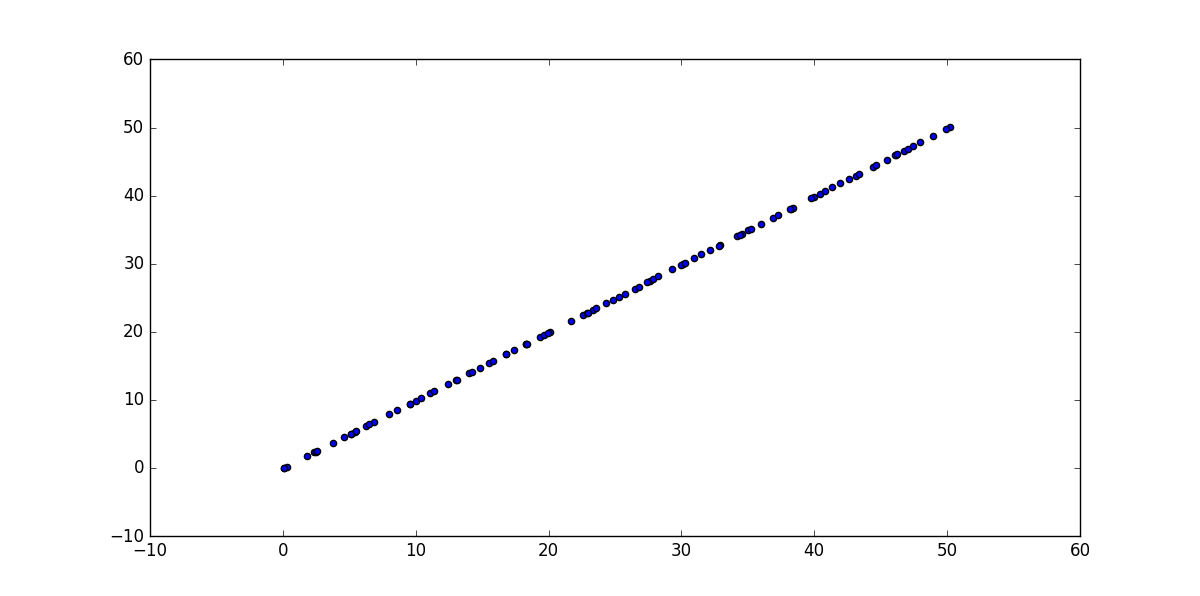
LDA
linear discriminant analysis线性判别分析
也是一种降维的方法,相比于pca为有监督降维算法,因为他需要类标的信息。通过$w$将$x_n$投影到一个一维的空间,使不同的类尽可能的分开。以两类为例,类1的中心点为
$$m_1 = \sum_{n \in C_1}x_n$$
类2的中心点为$$m_2 = \sum_{n\in C_2}x_n$$
为了使类分开,那么要是$m = w^Tm_1 - w^Tm_2$尽可能的大,因为我们只需要寻找到$w$的方法,上式可以让$||w|| \rightarrow \infty$达到最大,所以需要加一个约束$\sum_iw_i^2=1$
在两类尽可能分开的同时,我们还希望在类间的方法尽可能的小,也就是
$$v_1 = \sum_{n\in C_1}(w^Tx_n - w^Tm_1)^2$$
尽可能的小。对类2也是这样,最后得到一个综合的值
$$J = \frac{(w^Tm_1 - w^Tm_2)^2}{v_1^2 + v_2^2}$$
$w$关于$J$的导数为$$\frac{\partial J}{\partial w} = \frac{(w^TS_ww)S_Bw - (w^TS_Bw)S_ww}{(w^TS_ww)^2}$$
其中
$$S_B = (m_1 - m_2)(m_1 - m_2)^T$$
$$S_w = \sum_{n \in C_1}(x_n - m_1) + \sum_{n \in C_2}(x_n - m_2)$$
令导数为$0$,并注意到$S_Bw$与$m_1 - m_2$同方向,所以有
$$w \propto S_w^{-1}(m_1 - m_2)$$
得到$w$,然后再把约束加归一化一下就可以了。
实现代码:
LDA
原始的点: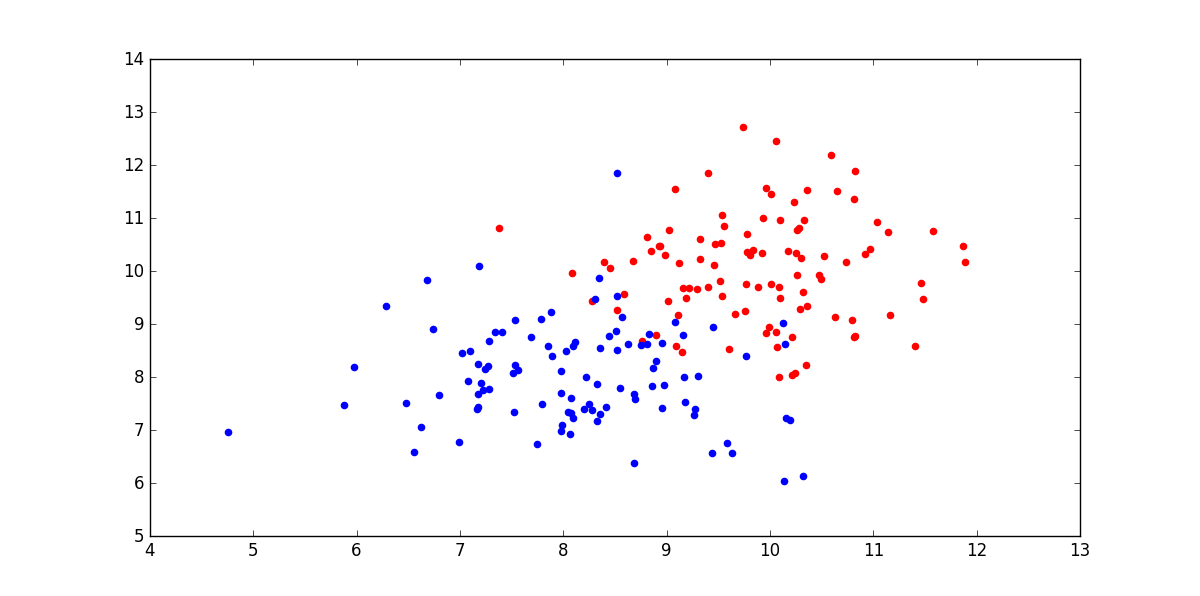
投影后的点:
Reference
PRML Chapter 12
PRML Chapter 4