对一些常用的采用进行总结，主要参考了PRML。

整个采样的关键思想：求
$$E[f] = \int f(z)p(z)dz$$

但是通常数值分析的方法很难求，寻求一种近似的方法
$$E[f] = \frac{1}{L}\sum f(z^{(l)})$$

其中$z^{(l)} \sim P(z)$，通常来说10~20个样本就可以很好的拟合，并且这个方法是不取决于z的维度的。

但是通常情况下，可能一些非常小概率的$z$决定了$E[f]$，所以可能要求采样数要采的比较多

对于有向图的采样，采用ancestral sampling。从父亲开始采样起。

如果观察节点固定的话，使用一种叫做logic sampling的方法。也是从父亲开始采样起，最终采样到可见节点，如果不符合的话，丢弃。

无向图的采样更加复杂，通常需要一些更复杂的采样方法，比如说吉布斯采样。

对于采样联合分布的边缘采样$p(u,v)$，如果我们要采样$P(u)$，简单的把$v$丢弃即可。

介绍一些常用的采样方法

Inverse CDF

最简单的采样，计算机只能生成一些伪随机数。在[0, 1]中均匀分布。现在假设计算机已经可以生成出[0,1]分布的样本$z$了，现在我们要从一个更复杂的分布$p(y)$中采出$y$，我们希望找到一个简单的映射
$y = f(z)$
$$p(y) = p(z)|\frac{dz}{dy}|$$
对于多元变量有
$$P(y_1,\cdots,y_m) =p(z_1,\cdots,z_m)\frac{\partial (z_1,\cdots,z_m)}{\partial (y_1,\cdots,y_m)}$$
Box-Muller变换
$z_1,z_2$从均匀分布中采样满足$z_1^2+z_2^2 \le 1$，那么有$p(z_1,z_2)=\frac{1}{\pi}$
接下来进行变换
$$y_1=z_1(\frac{-2\ln z_1}{r^2})$$

$$y_2=z_2(\frac{-2\ln z_2}{r^2})$$

现在$y_1,y_2$为均值为0，方差为1的独立高斯分布。
对于均值为$\mu$,方差为$\sigma$，使用$\sigma y + \mu$即可。如果是covariance $\Sigma$，使用Cholesky decomposition,$\Sigma = LL^T$，然后$y = \mu + Lz$

Rejection Sampling

为了从$p(z) = \frac{1}{Z_p}\tilde{p}(z)$中采出样本出来，通常$\tilde{p}(z)$是很好计算的，但是分母$Z_p$难以计算。我们提出一个分布$q(z)$，以及一个常数，其中满足$kq(z) \ge \tilde{p}(z)$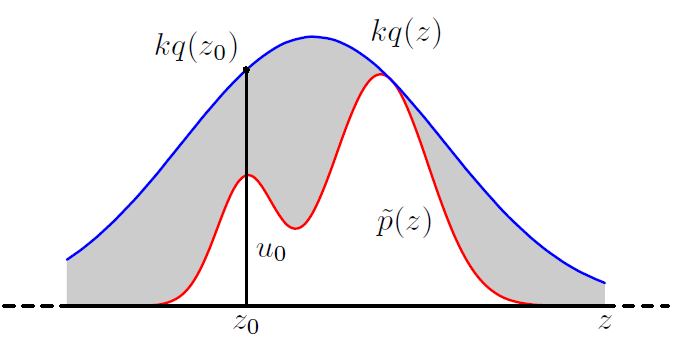

然后从$z_0 \sim q(z)$，所以接受率为
$$p(acc) = \int{\bar{p}(z)/kq(z)}q(z)dz = \frac{1}{k}\int\bar{p}(z)dz$$

Adaptive rejection sampling

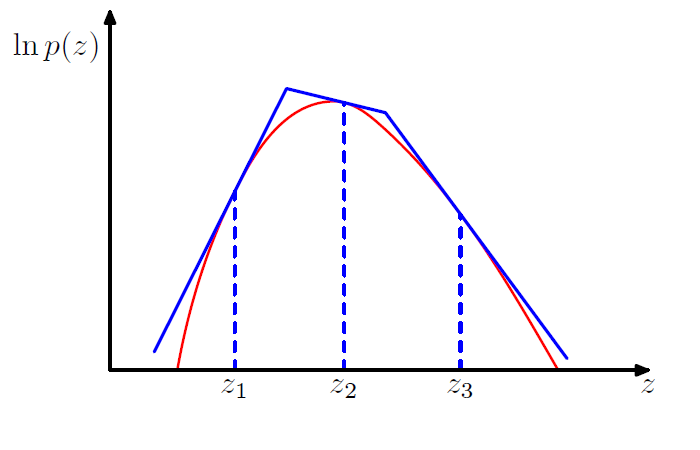
通常来说决定k是比较困难的一件事情，但是对于log凹的函数来说会比较的简单。
首先选取几个初始的点，算一下梯度，然后构造一些切线。因为在对数区是切线，所以对应的分布为
$$q(z) = k_i\lambda_i \exp(-\lambda_i(z - z_{i-1})) \quad z_{i - 1} < z \le z_{i}$$

然后按照正常的rejection sampling去做，如果当前点被接受了，不做任何修改。
如果当前点被拒绝了，就从这个点重新构造一条切线出来。
但是这个方法通常在高维空间有问题。比如说两个高斯$\sigma_p^2I$与$\sigma_q^2I$,对于D维来说，$k=(\sigma_q/\sigma_p)^D$，如果$\sigma_q$只高出0.01，那么最后接受率大概为$1/200000$

Importance sampling

前面的几种方法都是从分布中采出样本出来，现在我们要求一个期望。$E[f] = \frac{1}{L}\sum p(z^{l})f(z^{l})$。我们采用如下的形式
$$E[f] = \int f(z)p(z)dz = \int f(z) \frac{p(z)}{q(z)}q(z) = \frac{1}{L}\sum \frac{p(z^{(l)})}{q(z^{(l)})}f(z^{(l)})$$

通常来说$p(z)$无法计算，所以通常的情况是$p(z) = \bar{p}(z)/Z_p$
那么上式就变为

$$E[f] = \int f(z)p(z)dz = \int f(z) \frac{p(z)}{q(z)}q(z) = \frac{Z_q}{Z_p}\frac{1}{L}\sum \bar{r}_lf(z^{(l)})$$

$$\frac{Z_p}{Z_q} = \frac{1}{Z_q}\int \bar{p}(z)dz = \int \frac{\bar{p}(z)}{\bar{q}(z)}q(z)dz = \frac{1}{L}\sum \bar{r}_l$$
所以有$E[f] = w_l f(z^{(l)})$
其中$$w_l = \frac{\bar{r}_l}{\sum_m \bar{r}_m} = \frac{\bar{p}(z^{(l)})/q(z^{l})}{\sum_m \bar{p}(z^{(m)})/q(z^{(m)})}$$

Sampling-Importance-resampling

通常对于一般的$p(z)$来说，没有办法决定合适的k值，所以提出这种方法。
首先从$q(z)$里面采出$L$个样本，然后算出权重$w_1,\cdots,w_L$，然后再根据权重采出$L$个样本出来。这样可以保证采出的$L$个样本是近似服从于$p(z)$的。
如果$L\rightarrow \infty$，可以证明就是$p(z)$

首先概率分布函数为$$p(z\le a) = \sum_{l:z^{l} \le a}w_l =\frac{\sum_l I(z^{(l)} \le a)\bar{p}(z^{(l)})/q(z^{(l)})}{\sum_l \bar{p}(z^{(l)})/q(z^{(l)})}$$
当$L \rightarrow \infty$，替换和为积分，得到
$$p(z\le a) = \frac{\int I(z\le a){\bar{p}(z)/q(z)}q(z)dz}{\int {\bar{p}(z)/q(z)}q(z)dz} = \int I(z \le a)p(z)dz$$

当$q(z)$和$p(z)$越接近，得到的样本就越好，当$q(z)=p(z)$的时候，可以得到每个权重都是$\frac{1}{L}$

MCMC and Gibbs

这篇Blog写的很不错MCMC and Gibbs