SVM
Lagrange对偶问题
首先一个约束问题
$$\begin{cases}\min \ f(x) \\ s.t.\ \ g_i(x) \ge 0\\ \quad \quad h_j(x) = 0\end{cases}$$
该问题可以转化成为等价的问题,引入拉格朗日函数$$L(x, w, v) = f(x) - \sum_iw_ig_i(x) - \sum_jv_jh_j(x),w_i \ge 0$$
等价问题为
$$\mathop{\min}_{x}\mathop{\max}_{w,v}L(x,w,v)$$
因为对于$L(x,w,v)$如果有某个$x$不满足特定的约束,如$g_k(x) < 0$或者$h_k(x) \neq 0$,那么$\mathop{\max}_{w,v}L(x,w,v) = +\infty$,所以满足约束的时候$\max L(x,w,v) = f(x)$
所以原问题等价于
$$\mathop{\min}_{x}\mathop{\max}_{w,v}L(x,w,v)$$
另外该问题有对应的对偶问题,对偶问题为
$$\mathop{\max_{w,v}}\mathop{\min}_{x}L(x,w,v)$$
对偶问题的上界是原问题的下界。
证明如下:对于$w_i\ge 0, g_i \ge 0,h_j(x) = 0$,说明对任意的$v$和$w_i\ge0$都有下式成立
$$\mathop{\min}_{x}L(x,w,v) \le f(x)$$
那么就有$$\mathop{\max}_{w,v}\mathop{\min}_{x}L(x,w,v,) \le \mathop{\min}_{x}f(x) = \mathop{\min}_{x}\mathop{\max}_{w,v}L(x,w,v)$$
上面称为Lagrange对偶问题
对于SVM来说
SVM特有的性质:sparse solutions。
也就是对于原来的核方法,我们不需要计算每个$k(x_n,x_m)$,而只是需要计算少量的核就可以了。
另外SVM是一个凸优化问题,也就是说任何一个找到的局部极值都是全局极值。证明方法是采用一阶充分条件去证。(也可看做是一个二次规划问题?)
SVM推导如下,首先核心思想是max-margin,也就是最大化分离面间距。决策函数为$$y(x) = w^T\phi(x) + b$$
对于$y(x) \ge 0$分为正例$t = +1$,对于$y(x) < 0$,分为负例$t= -1$。所以对于可分数据集来说,最终的所有数据都满足$ty(x) \ge 0$
对于数据$x_i$来说,到分离面的距离为$$d_i = \frac{|w^T\phi(x_i) + b|}{||w||_2} = \frac{t_i(w^T\phi(x_i) + b)}{||w||_2}$$
所以目标函数为$$L = \mathop{\max}_{w}(\mathop{\min}_i \frac{t_i(w^T\phi(x_i) +b)}{||w||_2})$$
又因为$w = kw, b = kb$,不影响最终的分离面,所以我们可以令$\mathop{min}_{i}\frac{t_i(w^T\phi(x_i) +b)}{||w||_2} = 1$,然后对于$$\mathop{max}_{w}\frac{1}{||w||_2} = \frac{1}{2}\mathop{min}_{w}||w||_2^2$$
所以最终的L可以转化成为以下问题
$$\begin{cases}\min\quad \frac{1}{2}||w||_2^2 \\ s.t. \quad t_i(w^T\phi(x_i) + b) \ge 1 (1 \le i \le n)\end{cases}$$
对于有约束的极大化问题,我们对每个约束引入拉格朗日乘子$\alpha_i$,原问题转化为如下问题$$L(w, \alpha) = \frac{1}{2}||w||_2^2 - \sum_{i}\alpha_i(t_i(w^T\phi(x_i) + b) - 1),\alpha_i \ge 0$$
对$w,b$求偏导并令其等于0,得到
$$\frac{\partial L}{\partial w} = w - \sum_{i}\alpha_it_i\phi(x_i) = 0 \Rightarrow w = \sum_{i}\alpha_it_i\phi(x_i)$$
$$\frac{\partial L}{\partial b} = \sum_{i}\alpha_it_i = 0$$
将$w, b$代回原式,得到$$L(\alpha) = \sum_i\alpha_i - \frac{1}{2}\sum_{i}\sum_{j}\alpha_i\alpha_jt_it_j\phi(x_i)\phi(x_j)$$
所以原问题转化为如下二次规划问题
$$\begin{cases}\mathop{max}_{\alpha}\quad \sum_i\alpha_i - \frac{1}{2}\sum_{i}\sum_{j}\alpha_i\alpha_jt_it_j\phi(x_i)\phi(x_j) \\ s.t. \quad \alpha_i \ge 0 (1 \le i \le n)\\ \quad\quad\ \sum_{i}\alpha_it_i = 0\end{cases}$$
这是对于数据是线性可分的情况,如果数据线性不可分,则对每一个约束项引入一个引子$\xi_i$,原来的问题转化为以下问题:
$$\begin{cases}\min\quad \frac{1}{2}||w||_2^2 + C\sum_{i}\xi_i\\ s.t. \quad t_i(w^T\phi(x_i) + b) \ge 1 - \xi_i \quad (1 \le i \le n) \\ \quad\quad\quad \xi_i \ge 0\quad (1 \le i \le n)\end{cases}
$$
同理引入拉格朗日乘子,因为有两个约束项,所以引入$\alpha_i, \mu_i$,原问题转化为
$$L(w, b, \xi, \alpha, \mu) = \frac{1}{2}||w||_2^2 + C\sum_{i}\xi_i - \sum_{i}\alpha_i(t_i(w^T\phi(x_i) +b ) - 1 + \xi_i) - \sum_{i}\mu_i\xi_i$$
同理对$w, b, \xi_i$求导,并代入原式,得到如下二次规划问题
$$\begin{cases}\mathop{max}_{\alpha}\quad \sum_i\alpha_i - \frac{1}{2}\sum_{i}\sum_{j}\alpha_i\alpha_jt_it_j\phi(x_i)\phi(x_j) \\ s.t. \quad C \ge \alpha_i \ge 0 (1 \le i \le n)\\ \quad\quad\ \sum_{i}\alpha_it_i = 0\end{cases}$$
解决上述二次规划问题中实用的是SMO算法。思想是每次选两次$\alpha_i, \alpha_j$进行迭代。将整个问题转化为一个变量的二次函数问题,直接有最大最小值可解。
实现代码如下:SVM
效果图:对于可分数据集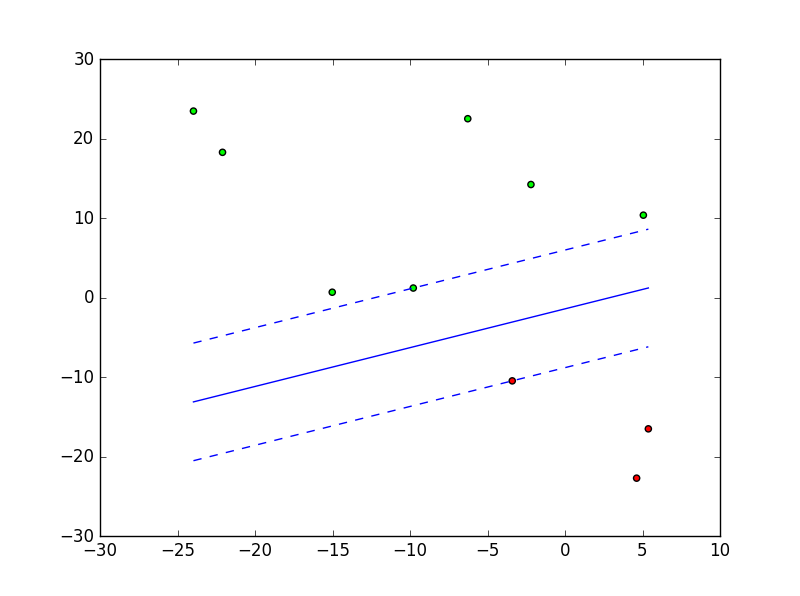
对于不可分数据集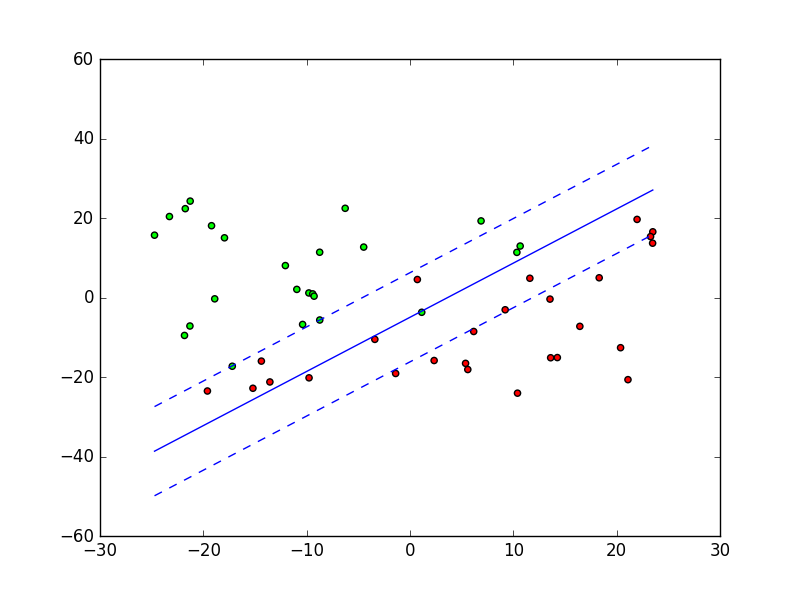
对于该代码有几个问题(主要参考了机器学习实战的写法)
1: 在初始选择j的时候如果返回的e_j有问题
2: 为什么要对E进行缓存
3: 对于一些线性可分的数据集最后画线的结果有问题 (待解决)